Módulo I.- Vectores en el espacio

Hola, bienvenid@s al módulo I.

En este módulo vamos a aprender a operar con los vectores de forma fácil y sencilla, para que pueda utilizarse este cálculo en los siguientes módulos del curso.

Vamos a empezar viendo qué es un vector.

Un vector, no es más que un segmento de una recta en el espacio que sale de un punto y llega a otro, es decir tiene origen, fin, dirección y sentido. $\vec{AB}= (x, y, z)$ .

Al hablar del espacio de $\mathbb{R}^{^{3}}$ ,todos los puntos y vectores vendrán representados por tres coordenadas, correspondientes a cada uno de los ejes coordenados.

Un vector $\vec{AB}$ nos indica que tiene su origen en el punto A y su fin en el punto B, para calcular sus coordenadas a partir de estos puntos origen y fin, tendremos que restar las coordenadas del punto final menos las del punto inicial ( se restan coordenada a coordenada, de tal forma que obtenemos el vector con sus tres coordenadas correspondientes, también.

Otro dato importante a conocer de un vector es cuánto mide, es decir, su módulo. Se representa como $\vec{AB}$

y se calcula de la siguiente manera: $\left | \vec{AB} \right | = \sqrt{x^{2}+y^{2}+z^{2}}$

Por ejemplo: Dados los puntos A = (1, 2, 3) y B = (-2, 1, 0); calcular el vector $\vec{AB}$ y su módulo:

$\vec{AB}$ = B-A = (-2, 1, 0) – (1, 2, 3) = (-2-1, 1-2, 0-3)= (-3, -1, -3)

$\vec{AB}$ = (-3) $\cdot$ 2+(-1) $\cdot$ 2+(-3) $\cdot$ 2 = 19

OPERACIONES CON VECTORES:

SUMA/RESTA DE VECTORES:

Para sumar y/o restar vectores operamos por coordenadas, es decir se suman o restan las coordenadas correspondientes a cada eje por separado. Sean los vectores

$\vec{a}= (a_{x}, a_{y}, a_{z})$ y $\vec{b}= (b_{x}, b_{y}, b_{z})$ , entonces $\vec{a\pm b} = (a_{x}\pm b_{x}, a_{y}\pm b_{z}, a_{z}\pm b_{z})$

Ejemplo: Dados los vectores

$\vec{a}$ = (1, -2, 1) y $\vec{b}$ = (-2, 1, -3). Calcula $\vec{a+b}$ y $\vec{a-b}$

$\vec{a+b}$ = (1, -2, 1) + (-2, 1, -3) = (1+(-2) , (-2)+1 , 1+(-3)) = ( -1, -1, -2)

$\vec{a-b}$ = (1, -2, 1) – ( -2, 1,-3) = (1-(-2) , -2-1 , 1-(-3) = (3, -3, 4)

PRODUCTO DE UN ESCALAR POR UN VECTOR:

Esta operación es bastante intuitiva, vamos a multiplicar el escalar (número) por todas las coordenadas del vector, quedando de la siguiente forma: $k\cdot \vec{v} = (k\cdot v_{x}, k\cdot v_{y}+ k\cdot v_{z})$

Ejemplo: $3\cdot \vec{a}$ = 3 (1, -2, 1) = (3, -6, 3)

PRODUCTO ESCALAR DE DOS VECTORES:

El producto escalar se define como: $\vec{a}\cdot \vec{b}= \left | \vec{a} \right |\cdot \left | \vec{b} \right |\cdot cos\alpha$ , siendo α el ángulo que forman los vectores a y b y pudiendo operarse $\vec{a}\cdot \vec{b}$ de la siguiente manera también: $\vec{a}\cdot \vec{b}= a_{x}\cdot b_{x}+a_{y}\cdot b_{y}+a_{z}\cdot b_{z}$

Hay que tener en cuenta que, del producto escalar, siempre vamos a obtener como resultado un número, nunca un vector.

Además este producto se usa muy frecuentemente, puesto que nos ofrece la ventaja de poder operarlo de una manera u otra.

Como ya te he comentado, el producto escalar es muy útil a la hora de trabajar con vectores. Voy a destacar algunas de las aplicaciones que más vas a usar:

Si dos vectores son perpendiculares (forman un ángulo de $90^{0}$ ), su producto escalar siempre va a ser igual a 0 (u $\vec{u}\perp \vec{v} \leftrightarrow \vec{u}\cdot \vec{v} = 0$ )
Si despejamos la parte del $cos\alpha$ , podremos obtener el ángulo que forman esos dos vectores ( $cos \alpha = \frac{\vec{u}\cdot \vec{v}}{\left | \vec{u} \right |\cdot \left | \vec{v} \right |}$ )
Nos permite calcular la proyección (sombra) de un vector sobre otro. La proyección del vector $\vec{u}$ sobre el vector $\vec{v}$ es igual a: $\frac{\left | \vec{u}\cdot \vec{v} \right |}{\left | \vec{v} \right |}$ (Lo trabajamos en valor absoluto, puesto que estamos dando una medida. Y el que va en el denominador siempre es el “sobre” )

Veamos unos ejemplos:

Sean los vectores $\vec{a} = (1, -2, 1)$ y $\vec{b} = (-2, 1, -3)$

$\vec{a}\cdot \vec{b}$ = 1 (-2) 1 + 1 (-3) = -7

Al no dar el producto escalar 0, podremos verificar que estos vectores no son perpendiculares. Averigüemos el ángulo que forman:

$cos \alpha = \frac{\vec{u}\cdot \vec{v}}{\left | \vec{u} \right |\cdot \left | \vec{v} \right |} = \frac{-7}{\sqrt{6}\cdot \sqrt{14}}$ = -0,76 ; = arccos (-0,76) = 139,8 grados

$\left | \vec{a} \right |= \sqrt{(1)^{2}+(-2)^{2}+(1)^{2}} = \sqrt{6}$

$\left | \vec{b} \right |= \sqrt{(-2)^{2}+(1)^{2}+(-3)^{2}} = \sqrt{14}$

Y por último vamos a calcular la proyección de $\vec{a}$ sobre el vector $\vec{b}$ es igual a: $\frac{\left | \vec{a}\cdot \vec{b} \right |}{\left | \vec{b} \right |}= \frac{7}{\sqrt{14}} = \frac{\sqrt{14}}{2}u$

PRODUCTO VECTORIAL DE DOS VECTORES:

El producto vectorial se define como: $\vec{a} x \vec{v}= \left | \vec{a} \right |\cdot \left | \vec{b} \right |\cdot sen \alpha$ , donde $\vec{a x \vec{b}}= \begin{vmatrix} \vec{i} & \vec{j} &\vec{k} \\ a_{x} & a_{y} & a_{z}\\ b_{x}& b_{y} & b_{z} \end{vmatrix}$ ; $\vec{i}, \vec{j}, \vec{k}$ hacen referencia a las coordenadas del eje x, y y z, respectivamente.

El producto puede resolverse como cualquier determinante de orden 3, por Sarrus o por adjuntos, como prefieras.

Voy a destacar algunas de las aplicaciones que más vas a usar:

del producto vectorial de dos vectores, se obtiene un vector perpendicular a ambos.
Si calculamos el módulo del vector obtenido, estaríamos calculando el área del paralelogramo definido por ambos vectores.
Si dividimos ese área entre dos, obtenemos el área del triángulo, de la mitad del paralelogramo.

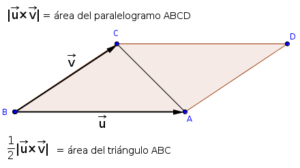
Veamos un ejemplo: Si tengo los vectores $\vec{a}= (1, -2, 1)$ y $\vec{b}= (-2, 1, -3)$

a) Calculamos el producto vectorial de ambos: $\vec{a}x\vec{b}=\begin{vmatrix} \vec{i} &\vec{j} &\vec{k} \\ 1& -2 &1 \\ -2&1 &-3 \end{vmatrix} = 6\vec{i}-2\vec{j}+\vec{k}-4\vec{k}+3\vec{j}-\vec{i}= 5\vec{i}+\vec{j}-3\vec{k}=(5, 1, -3)$

Este vector que henos obtenido sería perpendicular a $\vec{a}$ y a $\vec{b}$

b) Calculamos ahora el módulo del vector obtenido: $\left | \vec{a}x\vec{b} \right | = \sqrt{(5)^{2}+(1)^{2}+(-3)^{2}} = \sqrt{35} u^{2}$ , este valor correspondería al área del paralelogramo que forman ambos vectores

c) Si dividimos el área obtenida entre dos, obtenemos el área de medio paralelogramo, por tanto, del triángulo: $\frac{\left | \vec{a}x\vec{b} \right |}{2}= \frac{\sqrt{35}}{2}u^{2}$

PRODUCTO MIXTO:

El producto mixto se designa como $[\vec{u}, \vec{v}, \vec{w}] = \vec{u}\cdot (\vec{v}x\vec{w})$

De este producto también vamos a obtener un valor escalar (un número), que representa el volumen del paralelepípedo que definen los tres vectores.

Si lo dividimos entre 6, obtendríamos el volumen del tetraedro formado.

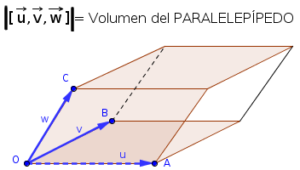
Veamos un ejemplo: Dados los vectores $\vec{a} = (1, 2, -1)$ , $\vec{b} = (-2, 1, -3)$ y $\vec{c} = (0, 1,2)$

Calcularemos su producto mixto, haciendo primero el producto vectorial de $\vec{b}$ y $\vec{c}$ y después el escalar del resultado con el $\vec{a}$

$\vec{b}x\vec{c}= \begin{vmatrix} \vec{i} &\vec{j} &\vec{k} \\ -2& 1 &-3 \\ 0&1 &2 \end{vmatrix} = 2\vec{i}+0\vec{j}-2\vec{k}-0\vec{k}+4\vec{j}+3\vec{i} = 5\vec{i}+4\vec{j}-2\vec{k}= (5, 4, -2)$

$[\vec{u}, \vec{v}, \vec{w}] = \vec{u}\cdot (\vec{v}x\vec{w})$ = (1, -2, 1) $\cdot$ (5, 4, -2) = 1 $\cdot$ 5 + (-2) $\cdot$ 4 + 1 $\cdot$ (-2) = -5

por último, te dejo un vídeo explicativo y además, en la pestaña de materiales, unos ejercicios para que vayas haciéndote amig@ de los vectores. A por ellos!

Módulo I.- Vectores en el espacio

Sobre Clases Ana:

Contacto

Sobre Clases Ana:

Contacto