Módulo I.- Campo Gravitatorio

Hola bienvenid@s a este primer módulo, aquí vamos a dar una vuelta por algunos conceptos del tema de campo Gravitatorio. NO olvides repasar también tus apuntes de clase

MÓDULO I.- CAMPO GRAVITATORIO

LEY DE GRAVITACIÓN UNIVERSAL:

Esta Ley establece que dos cuerpos de masas M y m, se atraen con una fuerza directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que las separa.

$vec{F_{g}}= frac{-GMm}{r^{2}}vec{u_{r}}$ . El signo negativo, solo lo usamos cuando trabajamos con la forma vectorial de esta fórmula, puesto que solo nos sirve para indicar que la fuerza es de atracción.

LEYES DE KEPLER: Son leyes empíricas acerca de las órbitas de los planetas en torno al Sol que se deducen a partir de la Ley de Gravitación Universal.

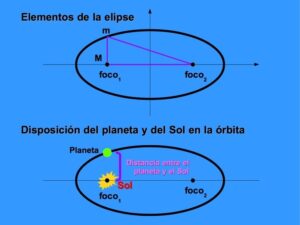
– PRIMERA LEY DE KEPLER (o de las órbitas planas) Establece que los planetas, en su movimiento alrededor del Sol, describen trayectorias planas, cerradas, de forma elíptica, en uno de cuyos focos se encuentra el Sol.

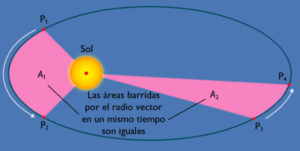
– SEGUNDA LEY DE KEPLER (ley de las áreas).- El radiovector, es decir la línea que une la posición del planeta con el Sol, barre áreas iguales en tiempos iguales. Es decir, la velocidad areolar se mantiene constante

$frac{dA}{dt}= constante$

– TERCERA LEY DE KEPLER (ley de los periodos).- El cuadrado de los periodos de los planetas es directamente proporcional al cubo de los semiejes mayores de la elipse que describen; T² = KR³, siendo K una constante igual para todos los planetas y que solo depende de la masa del Sol.

Deducción: Si tenemos un planeta, de masa m_p, que gira en una órbita circular en torno al Sol, de masa M_sol. Como la órbita es circular, describe un movimiento circular uniforme (MCU), por lo que se establece que:

Si está en órbita, debe haber un equilibrio, si no se saldría de esta. Tal y como enuncia la segunda Ley de Newton: $sum vec{F}= mcdot vec{a}$ , por lo que en este caso la F_g = m a_n

Dado que F_g = $frac{GM_{sol}cdot m_{p}}{r_{o}^{2}}$ ; la a_n = $frac{v^{2}}{r_{o}}$ ; T = $frac{2pi r}{v}$ y por tanto, v = $frac{2pi r}{T}$ Podemos decir que:

F_g = m a_n; $frac{GM_{sol}cdot m_{p}}{r_{o}^{2}}$ = $frac{v^{2}}{r_{o}}$ ; $frac{GM_{sol}cdot m_{p}}{r_{o}^{2}}$ = $frac{(frac{2pi r_{o}}{T})^{2}}{r_{o}}$ ; $T^{2}= frac{4pi ^{2}r_{o}^{3}}{GM_{sol}}$

Dado que los valores de 4, pi, G y M_sol son valores constantes, queda demostrado que $T^{2}= kcdot r_{o}^{3}$ , donde k = $frac{4pi ^{2}}{GM_{sol}}$

CAMPO GRAVITATORIO: Es la perturbación que genera un cuerpo por el hecho de tener masa. Va dirigido siempre hacia la masa que lo genera y es un campo conservativo.

Se representa por lo que llamamos líneas de campo, que son líneas que van dirigidas hacia la masa y además:

Son tangentes en cada punto al vector intensidad
Tienen el mismo sentido que el vector intensidad de campo
No tienen origen definido
Terminan en puntos que llamamos sumideros de campo
La densidad de las líneas de campo es proporcional al módulo de la intensidad de campo
Nunca se cortan, puesto que solo hay un vector intensidad de campo

La INTENSIDAD DEL CAMPO GRAVITATORIO, la genera una masa a una distancia determinada y es la fuerza gravitatoria que se ejerce sobre la masa unidad situada en dicho punto, es decir, es la fuerza gravitatoria por unidad de masa.

$vec{g} = frac{vec{F_{g}}}{m}= frac{-GMn/r^{2}}{m}= frac{-GM}{r^{2}}$

Por el principio de superposición, tanto la fuerza gravitatoria como la intensidad de campo gravitatorio totales, son la suma de todas las fuerzas o campos existentes.

ENERGÍA POTENCIAL: Una partícula de masa m, situada en un campo gravitatorio está sometida a la acción de fuerzas gravitatorias y debido a ello, posee energía potencial gravitatoria, de expresión: Ep = $frac{-GMm}{r}$ y cuyas características principales son:

Siempre es negativa
Su valor máximo será cero, cuando las masas estén alejadas una distancia infinita
También aplica el principio de superposición.

POTENCIAL GRAVITATORIO: es la energía potencial por unidad de masa, también es una magnitud escalar y su expresión es: V = $frac{-GM}{r}$ .

También cumple que en el infinito es cero y aplica el principio de superposición.

TRABAJO: El trabajo en campo gravitatorio solo depende de su estado inicial y final, no depende de la trayectoria.

W_AB = – (Ep_B – Ep_A) = -m (V_B-V_A)

Si el trabajo es positivo (W $> 0$ ),el proceso es espontáneo, lo realiza el campo

Si el trabajo es negativo(W $< 0$ ),el proceso no es espontáneo, lo realiza una fuerza exterior al campo.

Si el trabajo es nulo (W $= 0$ ), significa que la masa se está desplazando entre dos puntos de una superficie equipotencial, es decir, una superficie en la que todos los puntos tienen el mismo potencial.

SATÉLITES EN ÓRBITA: Cumplen que $sum vec{F}= mcdot vec{a}$ , demostrando como antes, llegamos a: $frac{GM_{sol}cdot m_{p}}{r_{o}^{2}}$ = $frac{v^{2}}{r_{o}}$ y por tanto, v₀ = $sqrt{frac{GM}{r_{o}}}$

Llamaremos satélites geoestacionarios a los que tienen un periodo de revolución igual al de la Tierra, es decir 24 horas.

VELOCIDAD DE ESCAPE: Es la velocidad mínima que debe adquirir un cuerpo para escapar de la atracción gravitatoria en cuyas proximidades se encuentre.

Por el principio de conservación de la energía: Ec_A + Ep_A = 0

$frac{1}{2}mv^{2}-frac{GMm}{r} = 0$ ; Despejando v llegamos a v = $sqrt{frac{2GM}{r}}$

ENERGÍA MECÁNICA DE UN SATÉLITE EN ÓRBITA:

E_M = E_C + E_P

E_M = $frac{1}{2}mv^{2}+frac{-GMm}{r} = 0$ . ; Si la v₀ = $sqrt{frac{GM}{r_{o}}}$

E_M = $frac{1}{2}m(sqrt{frac{GM}{r}})^{2}+frac{-GMm}{r} = 0$ ; E_M = $frac{1}{2}m{frac{GM}{r}}+frac{-GMm}{r} = 0$ ; E_M = $frac{-1}{2}{frac{GMm}{r}}$

Vuelve a aparecer el signo negativo, debido a la característica atractiva, de hecho, para que esté el satélite orbitando, la energía mecánica tiene que ser negativa.

Módulo I.- Campo Gravitatorio

Sobre Clases Ana:

Contacto

Sobre Clases Ana:

Contacto